확인했음
효율적인 데이터 관리의 핵심, 이진 트리와 이진 탐색 트리를 파이썬으로 마스터하세요! 이 글에서는 이진 트리와 이진 탐색 트리의 기본 개념부터 파이썬을 이용한 구현, 그리고 실제 활용 예시까지 꼼꼼하게 다룹니다. 알고리즘과 데이터 구조에 대한 이해도를 한 단계 끌어올릴 수 있는 완벽 가이드가 될 거에요!
이진 트리: 기본 개념부터 차근차근 알아보기

쉽게 말해, 각 노드가 최대 두 개의 자식 노드를 갖는 트리 구조를 이진 트리라고 합니다. 마치 나무처럼, 루트 노드에서 가지가 뻗어나가는 모습을 상상하면 이해하기 쉬울 거에요. 왼쪽 자식과 오른쪽 자식을 구분하는 게 이진 트리의 핵심 특징이죠. (물론, 자식 노드가 하나도 없거나, 하나만 있는 노드도 있을 수 있어요!)
이진 트리는 데이터를 계층적으로 표현하는 데 정말 유용해요. 파일 시스템이나 조직도를 생각해 보세요. 루트 디렉토리 또는 최고 경영진에서 시작해서, 하위 디렉토리나 부서로 계속 뻗어나가는 모습, 이게 바로 이진 트리 구조와 닮았죠! 덕분에 데이터 접근이나 관리가 효율적으로 이루어질 수 있어요. 게다가, 이진 트리를 기반으로 하는 다양한 알고리즘들이 존재한다는 사실! 알고리즘 설계의 기초가 되는 중요한 개념이라고 할 수 있겠네요.
이진 트리의 종류도 다양해요. 완전 이진 트리, 포화 이진 트리 등 여러 가지가 있는데요, 각각의 특징과 성질을 파악하는 건 다음 단계에서 좀 더 자세히 살펴볼게요. 자, 이제 이진 트리에 대한 기본적인 이해를 했으니, 다음 단계로 넘어가볼까요? 이진 탐색 트리의 세계로 말이죠!
이진 탐색 트리(Binary Search Tree, BST): 효율적인 탐색의 비밀
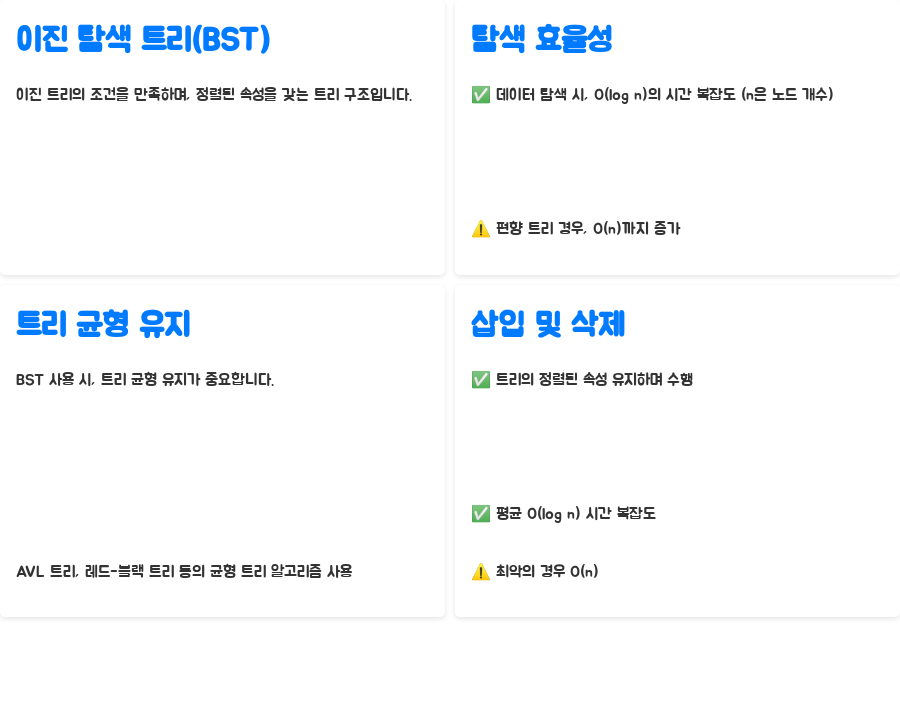
자, 이제 이진 트리의 특별한 형제, 이진 탐색 트리 (BST)를 만나볼 시간입니다! BST는 이진 트리의 조건을 만족하면서 동시에 특별한 규칙을 따르는 트리 구조에요. 바로, 정렬된 속성입니다. 어떤 노드를 보더라도, 그 왼쪽 서브트리에 있는 모든 노드의 값은 그 노드의 값보다 작고, 오른쪽 서브트리에 있는 모든 노드의 값은 그 노드의 값보다 커야 해요. (이게 핵심이에요!)
이 규칙 덕분에 BST는 데이터를 탐색할 때 엄청난 효율성을 보여줍니다. 데이터를 찾을 때, 일일이 모든 노드를 확인할 필요가 없어요. 찾고자 하는 값과 현재 노드의 값을 비교하고, 더 작으면 왼쪽 서브트리로, 더 크면 오른쪽 서브트리로 이동하면서 탐색하면 되거든요. 평균적으로 O(log n)의 시간 복잡도를 가지죠! (n은 노드의 개수) 와, 정말 빠르죠?
하지만, 최악의 경우에는 어떨까요? 만약 트리가 한쪽으로 심하게 치우쳐서, 일렬로 쭉 늘어선 모양이 된다면 (이런 경우를 편향 트리라고 해요), 탐색 시간 복잡도는 O(n)까지 증가할 수 있어요. 그래서, BST를 사용할 때는 트리의 균형을 유지하는 것이 매우 중요합니다. (균형 트리에 대한 이야기는 조금 더 심화 내용으로 다음 시간에 자세히 다뤄볼게요!) 이런 균형 유지를 위해 AVL 트리나 레드-블랙 트리와 같은 균형 트리 알고리즘을 사용하기도 하죠.
BST에서의 삽입과 삭제 연산도 마찬가지로, 트리의 정렬된 속성을 유지하면서 수행되어야 합니다. 그래서, 단순한 이진 트리보다 조금 더 복잡한 알고리즘이 필요하지만, 여전히 평균적으로 O(log n)의 시간 복잡도를 유지하기 때문에 매우 효율적입니다. (하지만 최악의 경우 역시 O(n)이 될 수 있으니, 균형 유지는 항상 중요해요!) 자, 이제 실제로 BST를 파이썬으로 구현해 보는 방법을 알아볼까요?
파이썬으로 이진 탐색 트리 구현하기: 실전 코딩!

자, 이제 본격적으로 파이썬 코드를 통해 BST를 구현해 봅시다. 우선, 노드(Node) 클래스를 정의해야겠죠? 각 노드는 값(value), 왼쪽 자식 노드(left), 오른쪽 자식 노드(right)를 저장합니다.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None, BST 클래스를 정의합니다. 메서드는 새로운 노드를 삽입하고, 메서드는 특정 값을 탐색합니다. 재귀 함수를 사용하여 코드를 간결하게 작성할 수 있어요. (저는 재귀 함수를 엄청 좋아하거든요! 😉)
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root is None:
self.root = Node(value)
else:
self._insert_recursive(self.root, value)
def _insert_recursive(self, node, value):
if value < node.value:
if node.left is None:
node.left = Node(value)
else:
self._insert_recursive(node.left, value)
else:
if node.right is None:
node.right = Node(value)
else:
self._insert_recursive(node.right, value)
def search(self, value):
return self._search_recursive(self.root, value)
def _search_recursive(self, node, value):
if node is None or node.value == value:
return node is not None # True if found, False otherwise
elif value < node.value:
return self._search_recursive(node.left, value)
else:
return self._search_recursive(node.right, value)
bst = BinarySearchTree()
bst.insert(8)
bst.insert(3)
bst.insert(10)
bst.insert(1)
bst.insert(6)
bst.insert(14)
bst.insert(4)
bst.insert(7)
bst.insert(13)
print(bst.search(6)) # True
print(bst.search(15)) # False코드를 직접 실행해보면서, BST의 동작 원리를 직접 확인해보세요!
이진 탐색 트리의 성능 비교: 균형 vs. 불균형
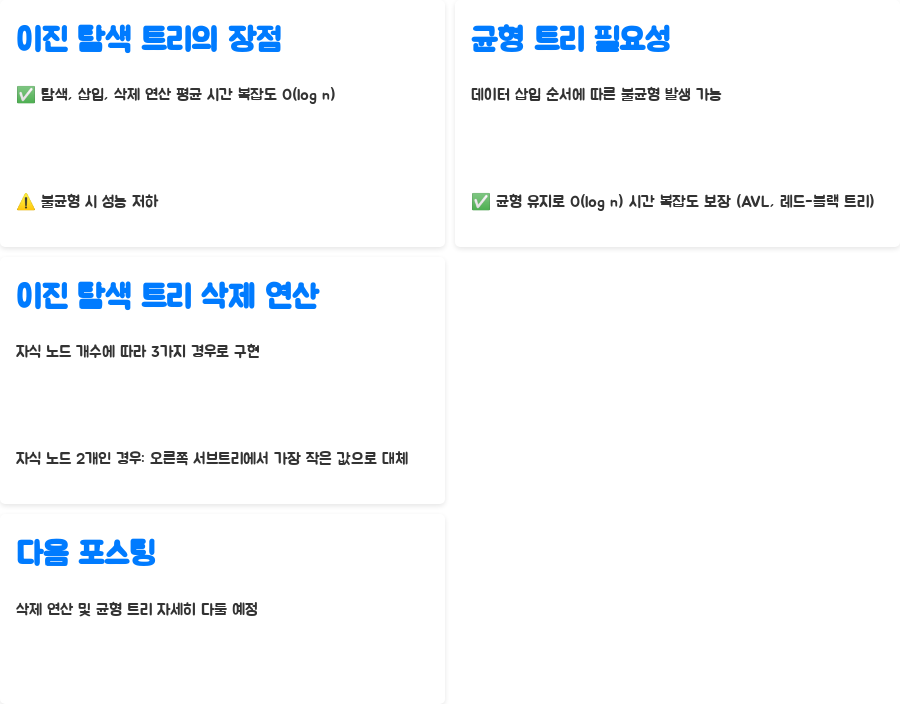
이진 탐색 트리의 성능은 트리의 구조, 즉 얼마나 균형이 잘 잡혀있는지에 따라 크게 달라집니다. 균형이 잘 잡힌 트리에서는 탐색, 삽입, 삭제 연산 모두 평균적으로 O(log n)의 시간 복잡도를 갖습니다. 하지만, 트리가 한쪽으로 치우쳐 불균형이 심해지면 최악의 경우 O(n)까지 시간 복잡도가 증가할 수 있어요.
| 균형 잡힌 BST | O(log n) | O(log n) | O(log n) | O(log n) |
| 불균형 BST | O(n) | O(n) | O(n) | O(n) |
트리 종류 탐색 시간 복잡도(평균) 삽입 시간 복잡도(평균) 삭제 시간 복잡도(평균) 최악의 경우 시간 복잡도
보시다시피, 균형 잡힌 BST는 불균형 BST에 비해 훨씬 효율적인 성능을 보여줍니다. 특히, 데이터의 양이 많아질수록 그 차이는 더욱 커지죠. 그래서 실제 응용 프로그램에서는 AVL 트리나 레드-블랙 트리와 같은 균형 잡힌 이진 탐색 트리 구조를 사용하는 경우가 많습니다.
자주 묻는 질문 (FAQ)
Q1: 이진 탐색 트리가 다른 자료구조보다 나은 점은 무엇인가요?
A1: 이진 탐색 트리는 탐색, 삽입, 삭제 연산의 평균 시간 복잡도가 O(log n)으로, 선형 리스트(O(n))보다 훨씬 효율적입니다. 특히, 데이터의 양이 많을 때 그 효율성이 더욱 두드러집니다. 하지만, 트리가 불균형일 경우 성능이 저하될 수 있다는 점을 기억해야 합니다.
Q2: 균형 트리(AVL 트리, 레드-블랙 트리)는 왜 필요한가요?
A2: 일반적인 이진 탐색 트리는 데이터 삽입 순서에 따라 트리가 한쪽으로 치우쳐 불균형이 될 수 있습니다. 이 경우, 탐색 시간 복잡도가 O(n)까지 증가하여 성능 저하를 야기합니다. 균형 트리는 트리의 균형을 유지하여 항상 O(log n)의 시간 복잡도를 보장합니다.
Q3: 이진 탐색 트리의 삭제 연산은 어떻게 구현하나요?
A3: 삭제 연산은 자식 노드의 개수에 따라 세 가지 경우로 나뉘어 구현됩니다. 자식 노드가 없는 경우, 하나인 경우, 두 개인 경우 각각 다른 알고리즘이 적용됩니다. 자식 노드가 두 개인 경우에는 삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 찾아서 삭제할 노드를 대체하는 방식이 일반적입니다. (다음 포스팅에서 자세히 설명해 드릴게요!)
마무리
이번 포스팅에서는 이진 트리와 이진 탐색 트리에 대해 자세히 알아보았습니다. 다음 포스팅에서는 삭제 연산과 균형 트리에 대해 더 자세히 다뤄보겠습니다!
키워드:파이썬,이진트리,이진탐색트리,데이터구조,알고리즘,자료구조,탐색,삽입,삭제,효율성,균형트리,AVL트리,레드블랙트리,코딩,프로그래밍,알고리즘분석,시간복잡도,재귀,데이터관리,계층구조



